I am a visual  learner and a doodler – I love to draw.  There is a freeing motion of putting all thoughts and feelings down, into not words, but visual representations.  Sometimes there may be nothing to make but swirls, but sometimes a carefully shaded hand or face becomes my artfully formed past time.

I always remember a love for drawing, and it was in middle school where this was further developed.  In middle school my teacher taught the art class all sorts of important information about accurate proportions that make drawings realistic, as well as line perspective.

I could talk about how a perfect human figure is all about the construction of proportions, but I mentioned some of the beauty in that as it relates to the Fibonacci sequence in a previous post. Instead, I mention Line Perspective.

 

I was sitting in Geometry last Monday and we dove into learning a new theorem, and therefore, a new proof.  This one is called Desargues’ Theorem which states:

Two triangles are in perspective if the lines joining corresponding vertices are concurrent.

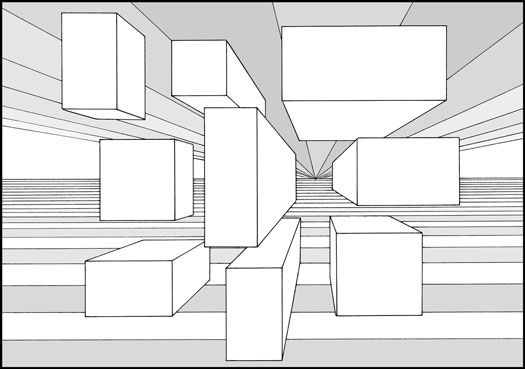
To which my professor began to draw two triangles “in perspective,” a visual  that greatly resembled my lessons in high school art class.  Basically, we’re learning about why techniques used in art class, techniques to make copies of life look real, can be justified reasonably with mathematics.

Then, there is a concept called duality for the relationship between points and lines.  Therefore, that comes down to how the theorem can be written a second way:

Two triangles are in point perspective if they are in line perspective.

It seems obvious, but that is a beauty of the mathematics.  That point at which two figures are in perspective, is the point of concurrency, or the point where the perspective lines meet.  In art this point is called the Vanishing Point because it is where  objects become too small to see.  As I was sitting in class, taking notes on this, I keep giving small gasps of excitement as I saw the math topic I most enjoy, geometry, explain the intricacies of the past time that I most love.  “*Gasp* This is beautiful!,” I exclaimed making my friend chuckle at my enthusiasm.